数据科学中的常见的6种概率分布（Python实现）

介绍

拥有良好的统计背景对于数据科学家的日常工作可能会大有裨益。每次我们开始探索新的数据集时，我们首先需要进行探索性数据分析(EDA)，以了解某些特征的概率分布是什么。如果我们能够了解数据分布中是否存在特定模式，则可以量身定制最适合我们的机器学习模型。这样，我们将能够在更短的时间内获得更好的结果(减少优化步骤)。实际上，某些机器学习模型被设计为在某些分布假设下效果最佳。因此，了解我们正在使用哪个概率分布可以帮助我们确定最适合使用哪些模型。

不同类型的数据

每次我们使用数据集时，我们的数据集都会代表总体的样本。然后使用这个样本，我们可以尝试了解其概率分布，以便我们可以使用它对总体进行预测。

假设我们要根据一组数据来预测房屋的价格，我们可以找到一个包含旧金山所有房价的数据集(我们的样本)，进行一些统计分析之后，我们就可以对美国其他任何城市的房价做出相当准确的预测(我们的总体)。

数据集由两种主要类型的数据组成：数值(例如整数，浮点数)和标签(例如名字，电脑品牌)。

数值数据还可以分为其他两类：离散和继续。离散数据只能采用某些值(例如，学校中的学生人数)，而连续数据可以采用任何实际或分数值(例如，身高和体重的概念)。

从离散随机变量中，可以计算出概率质量函数，而从连续随机变量中，可以得出概率密度函数。

概率质量函数给出了变量可以等于某个值的概率，概率密度函数的值本身并不是概率，需要在给定范围内进行积分。

自然界中存在许多不同的概率分布，在本文中，我将向大家介绍数据科学中最常用的概率分布。

在本文中，我将提供有关如何创建每个不同概率分布的代码。首先，让我们导入所有必要的库：

import pandas as pd 

import numpy as np 

import matplotlib.pyplot as plt 

import scipy.stats as stats 

import seaborn as sns 

伯努利分布

伯努利分布是最容易理解的分布之一，可用作导出更复杂分布的起点。这种分布只有两个可能的结果，一个简单的例子就是抛掷偏斜/无偏硬币。在此示例中，可以认为结果可能是正面的概率等于p，而对于反面则是(1-p)(包含所有可能结果的互斥事件的概率总和为1)。

probs = np.array([0.75, 0.25]) 

face = [0, 1] 

plt.bar(face, probs) 

plt.title('Loaded coin Bernoulli Distribution', fontsize=12) 

plt.ylabel('Probability', fontsize=12) 

plt.xlabel('Loaded coin Outcome', fontsize=12) 

axes = plt.gca() 

axes.set_ylim([0,1]) 

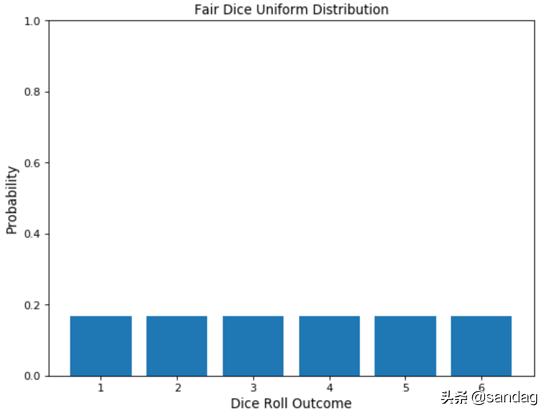
均匀分布

均匀分布可以很容易地从伯努利分布中得出。在这种情况下，结果的数量可能不受限制，并且所有事件的发生概率均相同。例如掷骰子，存在多个可能的事件，每个事件都有相同的发生概率。

probs = np.full((6), 1/6) 

face = [1,2,3,4,5,6] 

plt.bar(face, probs) 

plt.ylabel('Probability', fontsize=12) 

plt.xlabel('Dice Roll Outcome', fontsize=12) 

plt.title('Fair Dice Uniform Distribution', fontsize=12) 

axes = plt.gca() 

axes.set_ylim([0,1]) 

二项分布

二项分布被认为是遵循伯努利分布的事件结果的总和。因此，二项分布用于二元结果事件，并且所有后续试验中成功和失败的概率均相同。此分布采用两个参数作为输入：事件发生的次数和试验成功与否的概率。二项式分布最简单的示例就是将有偏/无偏硬币抛掷一定次数。

大家可以观察一下不同概率情况下二项分布的图形：

# pmf(random_variable, number_of_trials, probability) 

for prob in range(3, 10, 3): 

    x = np.arange(0, 25) 

    binom = stats.binom.pmf(x, 20, 0.1*prob) 

    plt.plot(x, binom, '-o', label="p = {:f}".format(0.1*prob)) 

    plt.xlabel('Random Variable', fontsize=12) 

    plt.ylabel('Probability', fontsize=12) 

    plt.title("Binomial Distribution varying p") 

（编辑：常州站长网）

【声明】本站内容均来自网络，其相关言论仅代表作者个人观点，不代表本站立场。若无意侵犯到您的权利，请及时与联系站长删除相关内容!